Research lines
• Laser Dynamics • Chaos Synchronization •
• Reservoir Computing • Complexity Measures •
LASER DYNAMICS
 Semiconductor lasers are known to be very sensitive to external perturbations such as feedback from a distant mirror, electrooptical feedback,
injection of light from another laser, delayed coupling, and current modulation. As a consequence of these perturbations, the laser's output emission may show complex dynamic behavior.
Semiconductor lasers are known to be very sensitive to external perturbations such as feedback from a distant mirror, electrooptical feedback,
injection of light from another laser, delayed coupling, and current modulation. As a consequence of these perturbations, the laser's output emission may show complex dynamic behavior.
In this research line, I concentrate on the influence of external optical feedback on the dynamical properties of semiconductor lasers, including the relaxation oscillation (RO) dynamics and delay-induced instabilities.
CHAOS SYNCHRONIZATION
 The study of synchronization in coupled dynamical systems dates back to the works of Huygens in the 17th century. When addressing synchronization in coupled complex dynamical systems, often the focus is on the particular case of an identically synchronized state. However, synchronization in a generalized sense can still exist, even if there is no one-to-one relationship between the responses of the coupled systems. Generalized synchronization requires a relationship between the dynamics of the constituting systems, no matter how complex this relationship is. If such a relationship exists, the response of one system is completely determined by the other one.
The study of synchronization in coupled dynamical systems dates back to the works of Huygens in the 17th century. When addressing synchronization in coupled complex dynamical systems, often the focus is on the particular case of an identically synchronized state. However, synchronization in a generalized sense can still exist, even if there is no one-to-one relationship between the responses of the coupled systems. Generalized synchronization requires a relationship between the dynamics of the constituting systems, no matter how complex this relationship is. If such a relationship exists, the response of one system is completely determined by the other one.
In this research line, I focus on the regimes of weak and strong chaos and its implications for the existence of (generalized) chaos synchronization.
RESERVOIR COMPUTING
 Reservoir computing (RC) is inspired by the way our brain appears to process information. In conventional RC, an untrained recurrent neural network forms the reservoir, which is read out by a simple external classification layer. This recurrent network can perform information processing by using the reservoir’s transient responses induced by an input signal. RC serves universal computational properties, i.e. any potential operation can be realized.
Reservoir computing (RC) is inspired by the way our brain appears to process information. In conventional RC, an untrained recurrent neural network forms the reservoir, which is read out by a simple external classification layer. This recurrent network can perform information processing by using the reservoir’s transient responses induced by an input signal. RC serves universal computational properties, i.e. any potential operation can be realized.
In the context of RC, simple delay systems can replace complex networks without losing functionality. Delay systems fulfill the required demands of high-dimensionality and they can be tuned to exhibit fading memory, two essential properties for RC.
In this research line, I explore the possibilities of using different non-linearities in the context of delay-based RC.
COMPLEXITY MEASURES
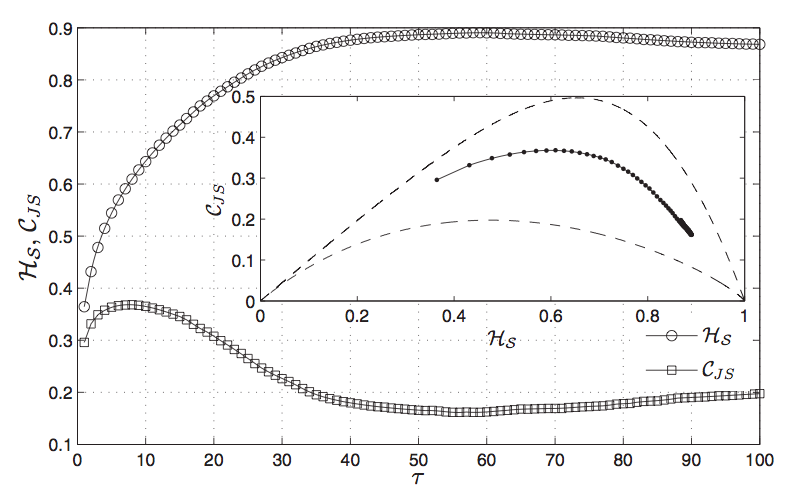 The task to distinguish between regular, chaotic, and stochastic dynamics from complex time series originating from experimental measurements can be a critical and subtle issue. Particularly, deterministic chaotic time series arising from high-dimensional nonlinear systems share several properties with those generated by stochastic processes, e.g., a wide-band power spectrum and a long-term unpredictable behavior. Moreover, experimental chaotic signals are unavoidably contaminated by noise, making the discrimination task even more challenging.
The task to distinguish between regular, chaotic, and stochastic dynamics from complex time series originating from experimental measurements can be a critical and subtle issue. Particularly, deterministic chaotic time series arising from high-dimensional nonlinear systems share several properties with those generated by stochastic processes, e.g., a wide-band power spectrum and a long-term unpredictable behavior. Moreover, experimental chaotic signals are unavoidably contaminated by noise, making the discrimination task even more challenging.
In this research line, I employ a reliable and computationally fast multiscale symbolic information-theory approach to identify the time scales where stochastic and nonlinear deterministic components govern the system's dynamics. In particular, complex multiscaled time series can be reliably characterized by estimating the permutation entropy and permutation statistical complexity as a function of the embedding delay.



