
MODASS
Modeling & Analysis of Social Systems _Research 
Temporal networks: slowing down diffusion by long lasting interactions
Oct. 19, 2013A new PRL paper recently published:
Interactions complex systems occur in a specific sequential order, thus affecting the flow of information, the propagation of diseases, and general dynamical processes. We investigate the Laplacian spectrum of temporal networks and compare it with that of the corresponding aggregate network. First, we show that the spectrum of the ensemble average of a temporal network has identical eigenmodes but smaller eigenvalues than the corresponding aggregate network. In large networks without edge condensation, the expected temporal dynamics is a time-rescaled version of the aggregate dynamics. Even for single sequential realizations, diffusive dynamics is slower in temporal networks. The discrepancies between aggregate networks and sequential interaction are due to the non-commutability of interactions. We illustrate our analytical findings using a simple temporal motif, larger network models and real temporal networks.
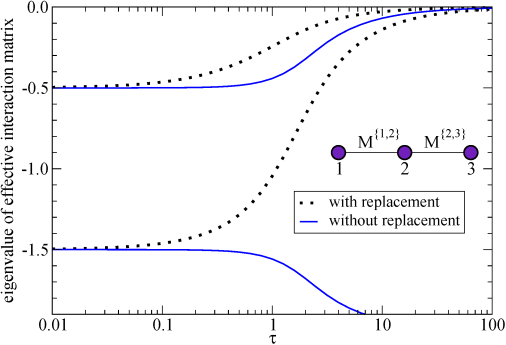
Spectrum of the effective interaction matrices as a function of interaction length τ. The two non-zero eigenvalues for a network with two edges connecting three nodes. Dotted, black curves: random sequences with replacement. Solid, blue curves: random sequences without replacement.
Collaboration with: Naoki Masuda (The University of Tokyo, Japan)
Konstantin Klemm (Leipzig University, Germany)

