Raúl Montagne, Maxi San Miguel, and Daniel Walgraef

Departament de Física, Universitat de les Illes Balears
E-07071 Palma de Mallorca, Spain
E.H-G e-mail address: dfsehg4@ps.uib.es



Antoni Amengual, Emilio Hernández-García,
Raúl Montagne, Maxi San Miguel, and Daniel Walgraef
Departament de Física, Universitat de les Illes Balears
E-07071 Palma de Mallorca, Spain
E.H-G e-mail address: dfsehg4@ps.uib.es
 On leave from
Université Libre de Bruxelles.
On leave from
Université Libre de Bruxelles.
The complex Ginzburg-Landau equation describes generically the amplitude of the unstable modes near a homogeneous Hopf bifurcation in spatially extended systems. It has been recently shown that a vector generalization of this equation is adequate for describing the dynamics of light polarization in some nonlinear optical systems [1]. An exploratory analysis of the behavior of this vectorial complex Ginzburg-Landau equation in the one-dimensional case will be presented here. Travelling and standing wave patterns, localized pulses, regimes of spatio-temporal intermitency and the consequences of a breaking of rotational symmetry will be described.
References



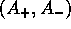 of the two unstable oscillating
vector modes at the lasing bifurcation of the above equations read:
of the two unstable oscillating
vector modes at the lasing bifurcation of the above equations read:
 ,
Which, after using (2), is of the form (1)
with
,
Which, after using (2), is of the form (1)
with  .
.
 and
and 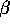 are the same as for the scalar two-level
model, and
are the same as for the scalar two-level
model, and
 .
.
 turns-out to be positive (Benjamin-Feir stable regime).
turns-out to be positive (Benjamin-Feir stable regime).

 of the TW solutions is linearly
unstable for
of the TW solutions is linearly
unstable for 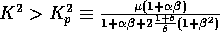 .
.
 and
and  of SW solutions are simultaneously
linearly unstable for
of SW solutions are simultaneously
linearly unstable for  .
.
 -plane centered in
the origin
beyond which they are phase-unstable. Our numerical analysis shows that TW
and SW unstable solutions evolves to other solutions of the same class and
smaller wavenumber through transient
depolarized states (FIGURE 2a) .
Unstable depolarized solutions evolve
in time to other states, which generically are also depolarized, through a
mechanism in which the circularly polarized
component of larger wavenumber reduces its wavenumber while the other component
remains stable (FIGURE 2b) .
-plane centered in
the origin
beyond which they are phase-unstable. Our numerical analysis shows that TW
and SW unstable solutions evolves to other solutions of the same class and
smaller wavenumber through transient
depolarized states (FIGURE 2a) .
Unstable depolarized solutions evolve
in time to other states, which generically are also depolarized, through a
mechanism in which the circularly polarized
component of larger wavenumber reduces its wavenumber while the other component
remains stable (FIGURE 2b) .
 close to 1, the main localized objects are circulary
polarized spots in a linearly polarized background.
close to 1, the main localized objects are circulary
polarized spots in a linearly polarized background.
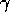 the chaotic dynamics of the two components
becomes strongly correlated (syncronized) (FIGURE 4)
.
the chaotic dynamics of the two components
becomes strongly correlated (syncronized) (FIGURE 4)
.
 -phase symmetry
(birrefringence, imperfections,...) leads to new phenomenology.
-phase symmetry
(birrefringence, imperfections,...) leads to new phenomenology.

 (
( if
if  ) these solutions destabilize, giving rise to TW with oscillating
propagation direction (FIGURE 5) .
) these solutions destabilize, giving rise to TW with oscillating
propagation direction (FIGURE 5) .


