Participant contribution
The extra invariant for Rossby waves and the emergence of zonal jets
- Author: Alexander M. Balk, University of Utah.
- Names of other authors: Francois van Heerden (South African Nuclear Energy Corporation, Pretoria 0001, South Africa), Peter B. Weichman (BAE Systems, Advanced Information Technologies, Massachusetts 01803, USA), Toshio Yoshikawa (Japan Science and Technology Agency, Japan).
- Oral or poster: oral.
- Downloadable abstract: click here.
- Downloadable presentation/poster: click here.
- Abstract:
The purpose of this talk is to show that the emergence of zonal jets (in atmospheres and oceans of rotating planets) follows from the presence of the extra conservation (like the inverse cascade follows from the conservation of the energy and enstrophy). We show that
- the Rotating Shallow Water dynamics has an adiabatic-type invariant
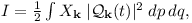
which is conserved approximately over long time; is the wave vector,
is the wave vector, 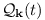 is the Fourier transform of the perturbational potential vorticity, and
is the Fourier transform of the perturbational potential vorticity, and 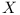 is the following function
is the following function
![X_{\bf k}=\frac{1}{p}\left[\arctan\frac{q+p\sqrt{3}}{k^2}-\arctan\frac{q-p\sqrt{3}}{k^2}] X_{\bf k}=\frac{1}{p}\left[\arctan\frac{q+p\sqrt{3}}{k^2}-\arctan\frac{q-p\sqrt{3}}{k^2}]](../images/e86d8c828ff7779aaa329b84a87d6fcf.png)
(the Rossby radius of deformation is normalized to 1); - the presence of this extra conservation implies that the inverse cascade transfers energy from small scale fluctuations towards large scale zonal jets (unless the forcinng wave-length significantly exceeds the Rossby radius).
- the Rotating Shallow Water dynamics has an adiabatic-type invariant